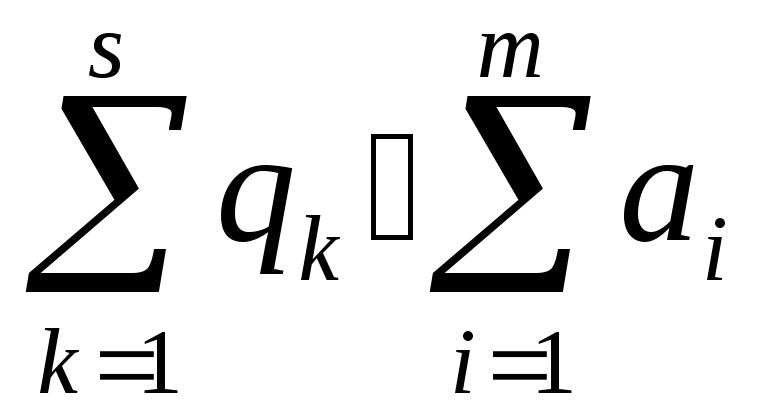Производимая продукция иногда проходит последовательную обработку нескольких предприятиях и в этом. случае необходимо комплексное решение проблемы размещения предприятий на всех стадиях. Кроме того, при размещении предприятий необходимо учитывать их зависимость от пунктов снабжения сырьем. В таких случаях приходится рассматривать многоэтапные модели размещения.
Рассмотрим простейший случай, когда система состоит из трех этапов: сырье — переработка — потребитель. Пусть имеется р сырьевых районов, n пунктов потребления и m возможных пунктов производства.
Qr — ресурсы сырья i -го района, (r = 1, p); ‘
Pj — объем потребления в j — м пункте, (j = ,n).
Известны также величины:
Сn — затраты на производство и доставку единицы сырья из r-го сырьевого района в i — й пункт производства;
Cij — затраты на производство единицы готовой продукции (без затрат сырья) в i -ом пункте и доставку в j — й пункт потребления;
W — норма расхода сырья на единицу готовой продукции.
Требуется найти неотрицательные переменные.
Xi — объем производства в i-м пункте;
Xij — объем перевозимой продукции из i-го пункта производства в .j — й пункт потребления;
Математическая модель задачи. Минимизировать
(3.34)
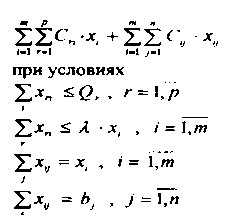
Ограничения модели характеризуют:
1- балансы распределения сырья по каждому сырьевому району;
2- балансы удовлетворения потребителей в сырье в каждом пункте производства;
3- балансы производства и распределения продукции в каждом пункте;
4- балансы удовлетворения потребностей в готовой продукции каждого потребителя.
В модели ограничения (1) — (4) комплексно решается проблема размещения предприятий с учетом их связей и с пунктами снабжения сырьем и с пунктами потребления готовой продукции.
Для задачи выполнено условие баланса ![]()
все сырье полностью перерабатывается, спрос всех потребностей удовлетворяется.
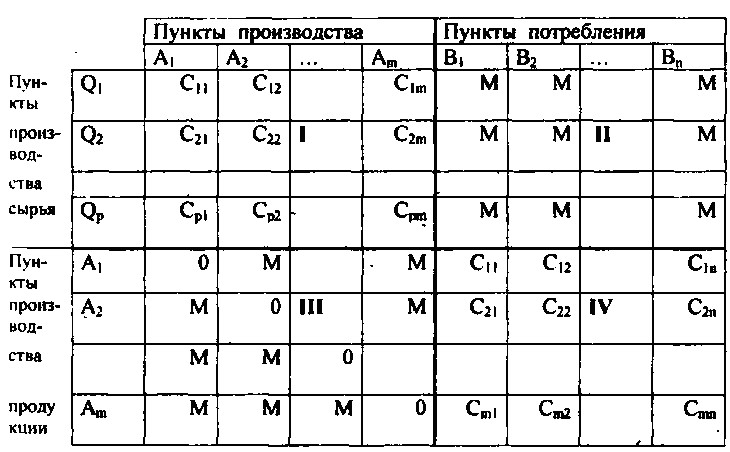
Задача решается по методу «фиктивной диагонали». Предприятия по производству продукции на первом этапе выступают потребителями сырья, на втором — поставщиками готовой продукции. Причем их мощности определяются из решения задачи. Задача решается в таблице (табл.3.1).
Табл. 3.1 состоит из четырех блоков. В 1-м блоке отражаются связи поставщиков сырья с перерабатывающими предприятиями. Во втором блоке — связи поставщиков сырья с потребителями готовой продукции. Поскольку потребителям необходима готовая продукция, эти связи запрещаются тарифами М -> + оо, что обеспечивает условие оптимальности для соответствующих клеток таблицы на всех этапах решения. Третий блок образуется строками и столбцами, относящимися к обрабатывающим предприятиям. Продукция перевозится потребителю, а не другому обрабатывающему предприятию, поэтому, связи предприятий друг с другом блокируются запретительными тарифами М. При любом расположении блоков, в таблице такие клетки будут представлять диагональ соответствующего блока. Ставя здесь нулевые тарифы, мы «разрешаем» сюда поставки. Они будут означать размер неиспользованной мощности соответствующего предприятия. Поскольку на самом деле поставки, указанные в этой диагонали, не осуществляются, они фиктивные, а сама диагональ называется фиктивной. В четвертом блоке отражаются связи пунктов производства продукции с пунктами потребления этой продукции.
Таблица 3.1
Метод «фиктивной диагонали»