Будем называть n-мерным вектором а упорядоченную последовательность чисел а1, а2,.., аn. При этом записывают a = (a1, a2,.., an).
ai — называют i-ой координатой вектора (i = 1,…, n), число n называют размерностью вектора. Вектор, все координаты которого равны нулю, называется нулевым.
Для векторов установлены понятия: равенства а = b, операции сложения (с = а + b), умножения на число (p = ta).
Два вектора называются равными, если равны их одноименные координаты. Вектор (-1)а называют противоположным и обозначают (-а). Вместо а+(-b) пишут а-b и называют это разностью векторов.
Действия с n-мерными векторами
- а(а1,а2,…,аn) + b(b1,b2,..,bn) = c(c1,c2,..,cn), где с1=a1+b1, c2=a2+b2,…, cn=an+bn, т. е. координаты вектора суммы нескольких векторов равны сумме их одноименных координат;
- Пусть ta = p, где t-число, тогда ta(а1,а2,…,аn) = p(tа1,tа2,…,tаn), т. е. умножение вектора на произвольное число равносильно умножению всех координат вектора на это число.
Операции сложения векторов, умножения вектора на число называют линейными операциями над векторами. Линейные операции над векторами обладают следующими свойствами (k и t -числа):
- a+b=b+a (переместительное свойство сложения).
- (a+b)+c=a+(b+c) (сочетательное свойство сложения).
- Если 0 — нулевой вектор, тогда а + 0 = 0.
- 1а = а.
- а + (-а) = 0.
- k(ta)=(kt)a (сочетательное свойство умножения);.
- (k+t)a=ka+ta (распределительное свойство относительно суммы чисел).
- k(a+b)= kа+kb (распределительное свойство относительно суммы векторов).
Рассмотрим операцию перемножения векторов. Существует скалярное, векторное и смешанное произведение векторов.
Скалярным произведением n-мерных векторов
a = (а1, а2,…, an) и b = (b1, b2,…, bn)
называют число, обозначаемое ab или (a,b), и равное сумме произведений одноименных координат векторов a и b:
(a,b) = a1b1 + a2b2 +… + anbn.
Скалярное произведение (а,а) = а2 = а2 называют скалярным квадратом.
Угол φ между двумя векторами a и b определяется соотношением
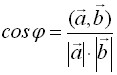
Спонсор статьи — копировальный центр «КопиМерк» г.Москвы — предлагает Вашему вниманию свои услуги по срочному широкоформатному копированию чертежей и документов, сканированию и брошюровке. Ваши заказы принимаются круглосуточно и будут выполнены оперативно в срок по доступным ценам.








