Построение общего решения системы линейных уравнений (метод Гаусса)

Весьма эффективным методом решения системы линейных уравнений, особенно с большим числом n-переменных и m-уравнений,является метод исключения неизвестных или метод Гаусса. (Здесь этот метод представлен в форме Жордана-Гаусса).

Общим решением совместной системы линейных уравнений называют равносильную ей разрешенную систему линейных уравнений.

Неизвестное x_j называют разрешенным, если какое-нибудь уравнение системы содержит x_j (j = 1,…, n) c коэффициентом 1, а во все остальные уравнения системы x_j не входит. Система называется разрешенной, если каждое уравнение содержит разрешенное неизвестное.

Метод Гаусса предполагает выполнение ряда действий, называемых элементарными преобразованиями. Хорошо отработайте на практике метод Гаусса, так как примеры с системными уравнениями ежегодно встречаются в ОГЭ по математике в 9 классе, в ЕГЭ в 11 классе и иных вступительных и выпускных экзаменах.

Элементарные преобразования допускают:

1. умножение обеих частей любого уравнения на некоторое число t, не равное нулю;
2. прибавление к обеим частям любого уравнения системы другого уравнения той же системы, умноженного на некоторое число t;
3. вычеркивание из системы тривиальных уравнений.

Рассмотрим систему линейных уравнений (1). Для удобства запишем в табличной форме коэффициенты при неизвестных и свободные члены. Зафиксируем неизвестное x_s и выберем в системе любое уравнение, содержащее это неизвестное. Пусть это будет уравнение с номером r и a_rs≠0.

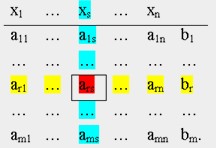
В дальнейшем будем называть x_s ведущим неизвестным, а коэффициент а_rs — ведущим элементом. Преобразование системы состоит из нескольких однотипных по процедуре шагов. На первом шаге выбирается ведущий элемент. В данном случае — это коэффициент a_rs. Уравнение с этим ведущим элементом (то есть уравнение с номером r) умножается на t = 1/a_rs. Далее последовательно к каждому из остальных уравнений системы прибавляется уравнение с номером r, предварительно умноженное на соответствующее каждому из этих уравнений число t_i = — a_is. Преобразованная система окажется, таким образом, разрешенной относительно ведущего (на этом шаге) неизвестного x_s. Если в результате преобразования в системе оказались тривиальные уравнения, их надо исключить.