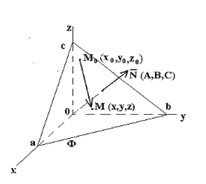
 Точка М(x,y,z) принадлежит плоскости Ф, если ее координаты удовлетворяют уравнению этой плоскости.
Точка М(x,y,z) принадлежит плоскости Ф, если ее координаты удовлетворяют уравнению этой плоскости.
Уравнение вида
![]()
называется общим уравнением плоскости. Плоскость будет задана, если заданы точка М0 (х0, y0, z0), принадлежащая плоскости, и координаты вектора , перпендикулярного данной плоскости (вектор называют нормальным вектором). В этом случае уравнение плоскости имеет вид ![]() (используется условие перпендикулярности векторов),
(используется условие перпендикулярности векторов),
![]() , следовательно, их скалярное произведение имеет вид
, следовательно, их скалярное произведение имеет вид ![]() , следовательно, их скалярное произведение имеет вид
, следовательно, их скалярное произведение имеет вид
Обозначив ![]() , получим общее уравнение плоскости
, получим общее уравнение плоскости
![]()
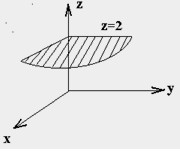
Рекомендация. Обратите внимание на частные случаи уравнений плоскости. Например, z = 2 — уравнение плоскости при А = 0 и В = 0. Расположение этой плоскости показано на рисунке. Другие случаи равенства нулю коэффициентов уравнения рассмотрите самостоятельно.
От общего уравнения можно перейти к уравнению в отрезках. Для этого выполним следующие действия.
![]()
Введя обозначения, получим уравнение, называемое уравнением плоскости «в отрезках на осях».
![]()
Величины a, b, c — отрезки, отсекаемые плоскостью соответственно на осях ОХ, ОY, OZ.
Пусть известны нормальные векторы двух плоскостей ![]() тогда из параллельности плоскостей вытекает параллельность векторов
тогда из параллельности плоскостей вытекает параллельность векторов ![]() тогда из параллельности плоскостей вытекает параллельность векторов
тогда из параллельности плоскостей вытекает параллельность векторов следовательно, их координаты пропорциональны.
![]() — это условие параллельности плоскостей.
— это условие параллельности плоскостей.
Если плоскости взаимно перпендикулярны, то ![]() то есть
то есть ![]() то есть
то есть — это условие перпендикулярности плоскостей.
Угол φ между плоскостями определяется как угол между нормальными векторами этих плоскостей. По формуле скалярного произведения векторов:
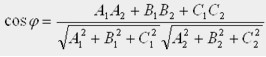
Пример
Написать уравнение плоскости Ф, проходящей через точки М1 (0,1,2) и М2 (1,-1,0) перпендикулярно плоскости![]() Построить плоскость Ф.
Построить плоскость Ф.
Решение: Напишем общее уравнение плоскости
![]()
Пусть вектор N={А,В,С} — нормальный вектор искомой плоскости,N 1= {2,-3,-1} — нормальный вектор известной плоскости. ПосколькуN перпендикулярен N1, то NN1 = 0, следовательно, 2A-3B-C=0
М1 и М2 принадлежат плоскости Ф, следовательно, их координаты удовлетворяют уравнению (2.2). Подставив в (2.2) координаты точек М1и М2, получим два уравнения
B+2C+D=0
A-B+D=0
Таким образом, получено три уравнения для четырех неизвестных А, В, С, D, а это значит, что необходимы дополнительные условия. Например, можно учесть, что длина вектора N может быть произвольной, тогда одну из координат, например, А можно положить равной единице. В результате получим систему уравнений

Таким образом, ![]() Полученные результаты позволяют написать уравнение искомой плоскости в виде
Полученные результаты позволяют написать уравнение искомой плоскости в виде ![]() Полученные результаты позволяют написать уравнение искомой плоскости в виде
Полученные результаты позволяют написать уравнение искомой плоскости в виде Для того чтобы построить плоскость, преобразуем полученное общее уравнение в «уравнение в отрезках»:
![]()
Если построение графиков вызывает у вас затруднение, можно воспользоваться онлайн сервисом построения графиков функций в прямоугольной системе координат, задав параметры оси X и Y и функцию.








