Рассмотрим трехмерные векторы. В отличие от многомерных они имеют наглядную геометрическую интерпретацию, поэтому традиционно, в соответствии с программой курса «Математика» сначала определяются понятия и операции, связанные с трехмерными векторами.
Вектором 
называют направленный отрезок 
называют направленный отрезок с началом в точке А и концом в точке В. Обозначают:
или или (в печатном тексте вектор обычно выделяют лишь жирным шрифтом, без черточки сверху).
Длина отрезка АВ называется длиной (модулем) вектора и обозначается 
или 
или .
Векторы, лежащие на одной или параллельных прямых, называются коллинеарными.
Два вектора и 
и равны, если они: коллинеарны, одинаково направлены, их длины равны. Таким образом, перенос вектора
параллельно самому себе в любое место пространства не изменяет вектора, поэтому все рассматриваемые здесь векторы будут свободными.
Рекомендация. Самостоятельно освоить: линейные операции над векторами (сложение, вычитание, умножение вектора на число); свойства линейных операций; определение проекции вектора на ось.
Проекция вектора на некоторую ось u вычисляется по формуле
где 
— косинус угла между вектором — косинус угла между вектором и осью u.
В дальнейшем проекции вектора на координатные оси будем обозначать: 
на координатные оси будем обозначать: или
. Если вектор задан координатами точек начала А(х1,у1,z1) и конца B(x2,y2,z2), то его проекции определяются по формулам ха = x2 — x1; уа = y2 — y1; za = z2 — z1.
Проекции вектора на координатные оси называются координатами вектора; соответственно приняты обозначения: ={X,Y,Z} или a(X,Y,Z)
Пусть 
— единичные векторы, то есть векторы единичной длины, совпадающие соответственно с направлениями координатных осей Ох, Оу, Оz.
Тройка векторов называется ортонормированным базисом трехмерного пространства. Любой трехмерный вектор может быть разложен по этому базису и представлен в виде = 
= . Причем это разложение — единственное в данном базисе, хотя сам ортонормированный базис является лишь одним из множества возможных базисов трехмерного пространства.
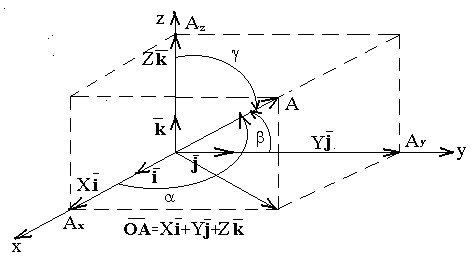
Непосредственно из рисунка (на основании теоремы Пифагора и определения косинуса угла) видно, что
;
Косинусы углов α, β, γ называются направляющими косинусами вектора
Спонсор статьи — онлайн сервис по решению задач по математике, физике, химии «Кто решит?», расположенный по адресу http://ktoreshit.ru/, поможет Вам стать отличником, ведь специалистам нашего портала любая задачка по плечу. Здесь вы также сможете найти себе помощника в написании диплома или курсовой работы и даже заработать, используя свой умственный потенциал.
