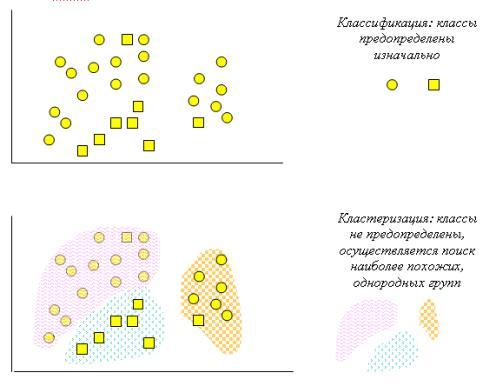
Классификация и регрессия
Постановка задачи.
В задаче классификации требуется определить значение зависимой переменной объекта на основании значений других переменных, характеризующих данный объект.
Пример: Информация о возможности проведения игр при разных погодных условиях.
Если значениями переменной являются значения конечного множества, то она имеет категориальный тип. Если множество значений переменной у конечна, то задача называется классификацией. Если же множество значений является множеством действительных чисел, то задача называется регрессией.
Представление результатов
1) Правило классификации.
ЕСЛИ (условие) ТО (заключение)
2) Деревья решений – это способ представления правил в иерархической структуре. Каждый узел дерева включает проверку первой независимой переменной. От дерева решений можно перейти к правилам. Преобразования от правил в деревьям не всегда возможно в связи с тем, что правила имеют большую свободу к записи.
3) Математические функции. В этом случае объекты рассматриваются как точки в м+1 мерном пространстве признаков. Если используются категориальные переменные, то они преобразовываются к числовому типу.
Построение правил классификации
Алгоритм 1-Rule
Для каждого возможного значения каждой независимой переменной формируется правило, которое классифицирует объекты из обучающей выборки. При этом в правой части указывается значение той зависимой переменной, которая наиболее часто встречается у объектов с выбранным значением независимой переменной, но не относящейся к выбранному классу. Если независимые переменные имеют вещественный тип, то количество возможных значений может быть бесконечно. Для решения этой проблемы всю область значений разбивают на интервалы, т.о.чтобы каждый из них соответствовал определенному классу.
Построение деревьев решений
Дерево решений строится при помощи рекурсивной процедуры.
Т- множество объектов на текущем шаге возможны 3 ситуации:
— Множество Т содержит один или более примеров, относящихся к одному классу, тогда Т – это лист.
— Множество Т пустое, тогда Т – лист, а класс этого листа выбирается из родительского множества.
— Множество Т содержит примеры, относящиеся к разным классам в этом случае Т нужно разбить на подмножества.
Существует несколько алгоритмов, строящих деревья, самые популярные – ID3, C4.5, CART.
ПРАВИЛО РАЗБИЕНИЯ.
Выбранный признак должен разбить признак так, чтобы полученные подмножества состояли из объектов, принадлежащих к одному классу или были максимально приближены к этому.
ПРАВИЛО ОСТАНОВКИ.
— ограничение глубины дерева
— полученное разбиение д.б.нетривиальным, т.е. полученные узлы должны создавать не менее заданного количества примеров.
ПРАВИЛО ОТСЕЧЕНИЯ.
Следует отсекать те ветви, которые не приводят к возрастанию ошибки.
АЛГОРИТМ ID3
Пусть Freg (Cq,T) – количество объектов из множества Т, относящихся к классу Cq. Вероятность того, что случайно выбранный объект будет принадлежать классу Cq:
Т по модулю – это мощность.
Среднее количество информации, необходим для определения класса объекта из множества 
:
, где К – число классов.
Среднее количество информации, необходимое для определения класса объектов после разбиения Т по переменной Х:
, где m – количество значений переменной Х.
Выбираем признак, по которому Gain будет больше.
Алгоритмы кластеризации
Имеется набор объектов 
, каждый объект задан набором признаков . Задача кластеризации состоит из построения множества 
, каждый объект задан набором признаков . Задача кластеризации состоит из построения множества , где
— это кластер, содержащий похожие друг на друга объекта из множества I.
, где 
, где — расстояние между объектами. G – величина, определяющая пороговое расстояние закл-ия объектов в 1 кластер.
Наиболее часто применяется Евклидовое пространство:
m=2
Агломеративный алгоритм
Агломерация – склеивание, объединение.
1)Все множество представляется как множество кластеров.
2)Выбираются 2 наиболее близких друг к другу из кластера и объединяются в один общий кластер.
3)Повторяется пока не останется требуемое число кластеров.
Под центром кластера понимается центр тяжести фигуры, состоящий из всех точек данного кластера. Он быстрее дивизионного алгоритма.
Дивизионный алгоритм
1)Помещаем все объекты в 1 кластер.
2)Выбирается элемент у которого среднее значение расстояния от других элементов в этом кластере наибольшее.
Условия остановки: получено требуемое число кластеров.
3)элемент в кластере С1 для которого разница между средним расстоянием до элемента находящегося в С2 и средним расстоянием до элементов остающихся в С1 наибольшее, переносится в С2.
Спонсор статьи — компания «IT-Gost» — предоставляет вашему вниманию информацию о различной технической документации, включая ГОСТы, международные стандарты и другую нормативную информацию.
