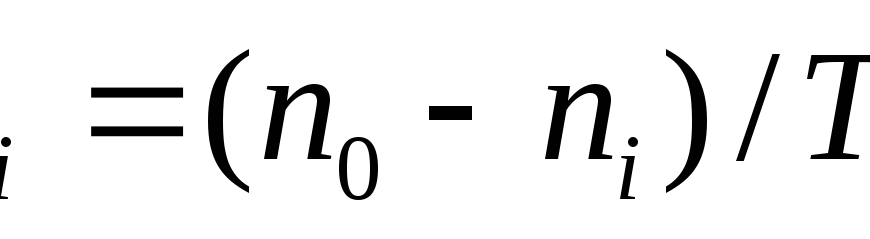Консолидацией платежей называется объединение нескольких платежей в один.
Сумма заменяемых платежей д.б. эквивалентна одному заменяющему платежу.
Пусть мы имеем серию платежей в размерах FV1, FV2, …, FVm с соответствующими сроками n1, n2,…,nm. Заменяем эту серию платежей на один платеж в размере FV0 и сроком уплаты n0. Величина FV0 неизвестна, но известен срок консолидированного платежа n0.
Для определения FV0 рассмотрим два варианта:
- Срок n0 находится внутри ряда n1, n2,…,nm, т.е. n1
0< nm. Пронумеруем платежи в интервале от n1 до n0 по j (FVj, nj), а в интервале от n0 до nm по к (FVк, nк). Тогда, разница в сроках определяется tj=n0-nj, tk=nk-n0. далее необходимо привести все платежи к единой временной точке. Возьмем в качестве такой точки время уплаты консолидированного платежа. Тогда
Первое слагаемое характеризует процессы наращения размеров платежей первоначальной серии, сроки уплаты которого д.б. наступить раньше срока консолидированного платежа.
Второе слагаемее выражает процессы дисконтирования размеров платежей, сроки которого наступают позже сроков консолидированного платежа.
- Для срока n0 верно n0>nm . В этом случае консолидированный платеж производится позже последнего платежа первоначальной серии уплаты платежа. Поэтому существует одна операция наращивания
![]()
Пример: два платежа со сроками уплаты 100 и 150 дней, и суммой 3 и 5 млн рублей заменяем 1 платежом со сроком 130 дней. Простая ставка 30%. Найти FV0.
FV0= 3*(1+0,3*30360)+5*(1+0,3*(150-130)360)-1=7,99 млн рублей.
Уравнение эквивалентности для сложной ставки
![]()
Пример: Платежи 1 и 2 млн руб со сроками уплаты через 1 и 2 года, заменяются 1 платежом через 1,5 года. Сложная ставка 20%. Найти FV0.