Псевдослучайные числа могут быть использованы в качестве исходного материала для моделирования любых вероятностных объектов (случайные события и связанные с ними процессы).
Пусть событие а имеет вероятность р(а), тогда процедура его моделирования с помощью равномерного распределения (0,1) чисел производится следующим образом:
- Выбирается очередное случайное число равномерно — распределенное.
- Проверка неравенства Xi≤p(a), устанавливается принадлежность X ε (0,p(a)]. Если неравенство выполнено, то событие а – наступило, в противном случае нет.
Аналогично выглядит процедура распределения дискретной величины с заданным законом распределения. Известен закон распределения случайной величины.
Z=(a1,a2,an)(p1,p2,pn) а1, а2, … — дискретные величины!!! р1, р2, … -вероятность дискретных величин
Разобьем (0,1) на n-интервалов, причем длины интервалов выберем равные вероятностям дискретных величин.
![]()
Моделирование сводится к следующему: для получения очередного значения Z, разрабатывается равное значение Xi , при попадании этого числа в j-интервал значение Z=Zi.
Все разнообразие методов получения случайных величин можно разделить на 2 группы: точные и приближенные методы.
- Пусть равномерно-распределенная величина в интервале [0;1] – X, получается из случайной величины Y с помощью неслучайной f-x=η(y), тогда очевидно следующее равенство: P(x
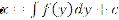
По определению ![]() первообразная, f(y) – интегральная функция распределения случайной величины у.
первообразная, f(y) – интегральная функция распределения случайной величины у.
Найдем функцию η(y) совпадающую с интегральным законом: η(y)=F(y)
Для получения очередного значения yi случайной величины Y рассмотренной в интервале (а,в), с законом распределения –f(y) соответствующему значению xi, необходимо решить уравнение. ![]() .
.
Подобная методика находит ограниченное применение, в связи с двумя обстоятельствами:
1.Для многих законов распределения интеграл правой части распределения в конечном виде не берется
2.Даже если удается взять интеграл правой части в конечном виде, то формулы получаются слишком громоздкими, требующих больше затрат машинного времени.








