Приближенные методы получения случайных чисел с заданным законом распределения
Поэтому чаще всего используются на практике приближенные методы. Рассмотрим один из универсальных приближенных методов. Пусть закон распределения случайной величины –y предложенный для моделирования заданной функции плотности – f(y) возможного значения принадлежащего (а,в) (если интервал с бесконечными границами, то целесообразно перейти к усеченному распределению, оставив лишь существенную часть).
Представим f(y) в виде кусочно-постоянной функции на отрезке [а,в], т.е. разобьем отрезок (а,в) на n-равных отрезков и будем считать значение f(y) на каждом отрезке величиной постоянной.
Т.е. случайную величину Y можно представить в виде Y=ak+xk, т.е. на каждом участке (ak,ak+1) величина xk считается постоянной, т.е. равномерно распределенной. Чтобы уточнить значение f(y) наиболее удобным способом целесообразно разбить (а,в) т.о. чтобы вероятность попадания случайной величины Y была постоянной, т.е. не зависела от некоторого интервала К. Для отчисления пользуются следующим соотношением: , где n- количество интервалов (n=2m).
Процедура моделирования предполагает следующее:
1.Выбирается случайное равномерно-распределенное число хк.
2.С помощью хк выбирается интервал (ак,ак+1)
3.Берется следующее равномерно-распределенное число xi+1 и масштабируетсяс целью приведения к интервалу (ак,ак+1), т.е xi+1 становится случайной величиной равномерно-распределенной в интервале (ак,ак+1). Т.о. случайное число yi находится по формуле: yi=ak+xi+1*(ак+1-ак)
Рассмотрим процесс выборки интервала (ак,ак+1) с помощью xi: случайное число xi получается с помощью ПК в виде последовательности 0 и 1, если m –разрядность двоичного числа, то всего двоичных чисел будет равно 2m и каждому интервалу разумно поставить одно двоичное число.
Особенность приближенных методов: для реализации данного метода на ЭВМ требуется небольшое количество операций, причем число операций не зависит от точности уточнения значений, т.е. не зависит от числа интервалов. Она влияет только на размеры участка памяти, куда помещаются таблицы закодированных значений ак.
Метод Неймана «разыгрывание» случайной величины
Нейман предложил способ получения заданного закона распределения, не требующий интегрального распределения и явлению точным, т.е. неиспользуемых приближений. Метод основан на имитационном моделировании закона распределения.
Пусть х- случайная величина распределенная на интервале (а,в) и моделируемая плотность ограничена М0. Выбираем 2 значения: r1, r2 – равномерно-распределенные в [0;1] случайной величины r. На плоскости f(y) и y наложим точку N с координатами (α,β).
N(α,β) α=a+r1(b-a) β=r2*M0
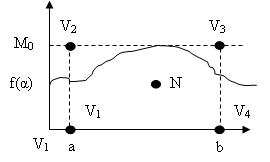
Если N лежит под кривой значит β
Если N называется кривой, то пара r1 и r2 отбрасывается и генерируется новая пара значений r3 и r4 . Предположим, что указанный способ приводит к закону распределения f(x). Т равномерно-распределена в CS=(b-a)*M0. Вероятность того, что N окажется ниже кривой N(x) равна отношению: 
, A – вероятность того, что точка окажется под кривой и в интервале (a|, b|):
, A – вероятность того, что точка окажется под кривой и в интервале (a|, b|):
Т.о. среди всех точек перешедших в х, доля попавших в интервал (a|, b|) = B/A=
.
Спонсор статьи — онлайн калькулятор Semestr — предлагает вашему вниманию сервис анализа оценки с помощью метода медиан рангов. Медианный метод оценки удобен для определения усредненных значений полученных случайных числел, а медианный калькулятор является удобным инструментом в случаях, когда число оцениваемых элементов является очень большим или случайным.
