Решение систем линейных уравнений с помощью определителей

Для простоты рассмотрим решение систем из трех уравнений с тремя неизвестными, хотя этот метод применим также к системам с большим числом уравнений и неизвестных. Для упрощения записи индексов в данном случае введем следующие обозначения: для переменных — x, y, z, для коэффициентов — a_i, b_i, c_i; для свободных членов — h_i, (i = 1, 2, 3):

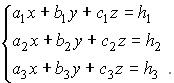(рис.1)

Все коэффициенты и свободные члены заданы. Если все свободные члены равны нулю, то система называется однородной.

В ходе решения будут использованы следующие определители:

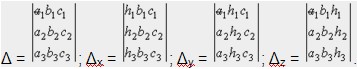
Δ называется определителем системы, определители Δ_x, Δ_y, Δ_z — вспомогательными определителями. Δ_x, Δ_y, Δ_z получаются из определителя системы путем последовательны заменой элементов первого, второго, третьего столбцов свободными членами.

При решении системы (рис.1) возможны два случая: Δ≠0 и Δ=0.

Если Δ≠0, то система имеет одно единственное решение, вычисляемое по формулам Крамера. (С выводом этих формул следует познакомиться по учебнику.)

Если Δ=0, то формулы Крамера теряют смысл. В этом случае система несовместна либо имеет бесчисленное множество решений. Очевидным признаком несовместности системы является отличие от нуля хотя бы одного из вспомогательных определителей — Δ_x, Δ_y, Δ_z. Действительно, тогда хотя бы одно из соотношений формул Крамера противоречиво.

Таким образом, можно сформулировать условия совместности и определенности системы линейных алгебраических уравнений:

Если Δ не равно нулю, система имеет единственное решение (определенная система);
Если Δ и все вспомогательные определители равны нулю, имеется бесконечное множество решений (неопределенные системы);
Если Δ=0, но хотя бы один из вспомогательных определителей не равен нулю, система несовместна (решений нет).

Пример 3.2. Решить систему с помощью формул Крамера

Применив формулы Крамера, получим

Следует обратить внимание на решение однородной системы линейных уравнений (свободные члены всех уравнений равны нулю). Очевидно, что такая система всегда имеет нулевое решение. Это решение единственное, если Δ не равно нулю (в соответствии с формулами Крамера). Если Δ=0, система имеет множество решений.

Рассмотрим решение однородной системы алгебраических уравнений с помощью определителей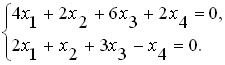

Так как определитель должен иметь равное число строк и столбцов, дополним недостающие строки нулевыми элементами. Определитель такой системы

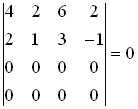
Все миноры четвертого и третьего порядка также равны нулю.

Найдем хотя бы один минор второго порядка, отличный от нуля. Например,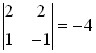

На базе этого минора перепишем систему в виде

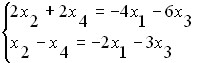
В левой части системы уравнений оставлены только те неизвестные, коэффициенты которых вошли в данный минор. Так как определитель этой системы не равен нулю, можно применить формулы Крамера

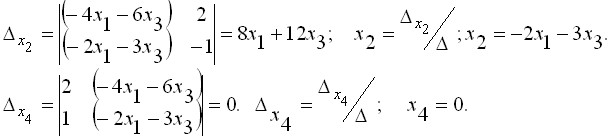
Положив х₁=λ₁, х₃=λ₂, где λ₁, λ₂ — произвольные числа, получим множество решений системы уравнений:

х₁ = λ₁, х₂ = 8λ₁+ 12λ₂, х₃ =λ₂, х₄=0.

Следует отметить, что решение этой системы методом Жордана-Гаусса будет существенно проще.

Спонсор статьи — библиотека знаний SekLib — предлагает Вам книги, учебники, пособия и многое другое для успешной сдачи экзаменов. Подробнее вы можете ознакомиться здесь — http://seklib.ru/ege-matematika/posobiy-ege.html