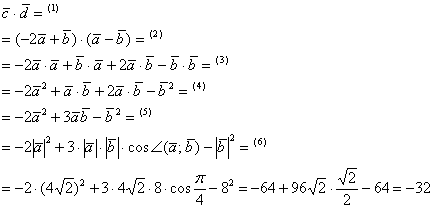Решение задач по теме Элементы векторной алгебры. Склярное произведение векторов

Скалярным произведением векторов  и и называется число (скаляр), равное произведению их длин, умноженному на косинус угла между ними, т. е.

Рекомендация. Познакомьтесь со свойствами скалярного произведения векторов и обратите внимание на то, что

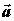
1. если  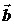(соs φ = 0), то 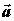(соs φ = 0), то 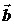= 0. Очевидно, что тогда и 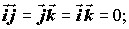= 0. Очевидно, что тогда и 
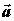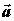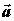
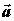
2. если вектор  умножается скалярно на вектор   умножается скалярно на вектор  (соs φ = 1), то  = а², следовательно, при скалярном перемножении одноименных ортов получим  .

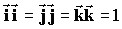Если векторы заданы своими координатами   (X₁,  Y₁, Z₁) и  (X₁,  Y₁, Z₁) и  (X2,  Y₂, Z2), то их скалярное произведение равно 

^**= x₁x₂+y₁y₂+z₁z₂

Если , то  x₁x₂+y₁y₂+z₁z₂ = 0 (условие перпендикулярности двух векторов). Угол между векторами определяется по формуле

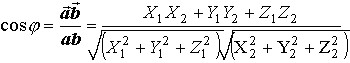
Пример 1

Заданы векторы 

 Разложить геометрически и аналитически вектор 

Решение.

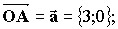
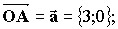
1. Запишем координаты векторов   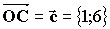  и построим векторы.

Разложить вектор  по векторам  по векторам  и , означает представить , означает представить  как сумму двух векторов, то есть представить   как результат линейных операций с векторами  как результат линейных операций с векторами  и    (говорят:    (говорят:  — линейная комбинация векторов  и  и  )

(п. 4)

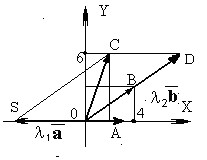
1. Сначала решим задачу графически:

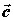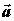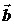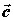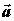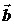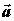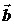   Из (п. 4) следует, что  — диагональ параллелограмма, построенного на векторах  — диагональ параллелограмма, построенного на векторах   и , следовательно, из конца вектора , следовательно, из конца вектора  проведем две прямые, параллельные соответственно  и и , продолжим линии векторов   и  и  (то есть ОА и ОВ) до пересечения с ними. Стороны полученного параллелограмма и есть искомые векторы 

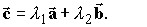
2. Аналитически решить данную задачу — значит найти из уравнения (1) значения λ₁ и λ₂, что позволит определить векторы 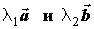. Выражение (1) с учетом условия задачи имеет вид 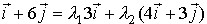. Выражение (1) с учетом условия задачи имеет вид  , отсюда, сгруппировав правую часть относительно i и j, получим 

Сравнение коэффициентов при  i и j, стоящих слева и справа в последнем выражении, позволяет записать систему уравнений относительно λ₁ и λ₂:

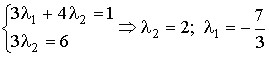
Таким образом, .

Пример 2

Известны точки А (0, 2, 3) и В (0, 1, 4), а также векторы  и  и , ; причем |; причем ||=2;  ; (b — угол  ; (b — угол с осью Оу). Найти вектор   и угол между векторами  и угол между векторами  и .

Решение:

1. Представим векторы 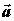 ,  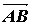,  и 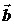координатами: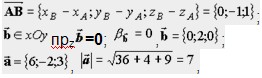
2. 

 следовательно

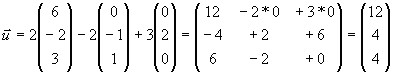
таким образом  ū=12i^→+4j^→ +4л^→

3. Из формулы скалярного произведения векторов  и и  следует:

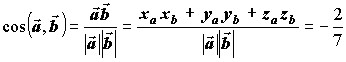
Спонсор статьи — компания UFAGIDRA — ваш сектрет успешной учебы, ведь специалисты компании всегда готовы помочь вам с расчетно-графическими задачами, курсовыми по гидравлике. Разумно используйте свое время! Если вы по каким-либо причинам не можете или не успеваете с домашним заданием, оставьте решение задач по гидравлике специалистам.