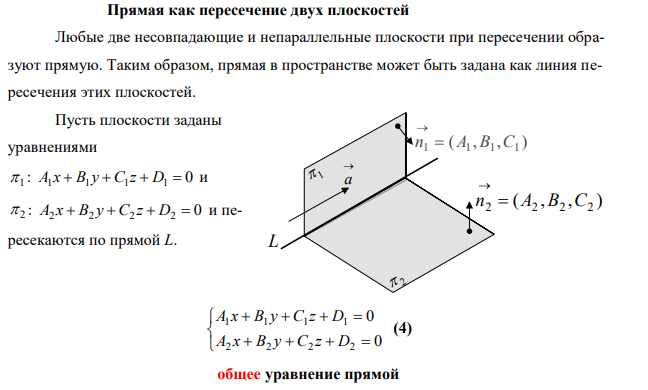
Уравнение прямой в пространстве задается в нескольких формах:
1. Общее уравнение прямой ![]()
2. Уравнение прямой, проходящей через данную точку М1 (х1, y1, z1) в заданном направлении вектор а = {l, m, n}. Пусть точка М (х, у, z) принадлежит прямой. Вектор ![]() параллелен вектору а, тогда
параллелен вектору а, тогда
по условию параллельности векторов их координаты пропорциональны.
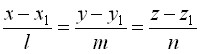
Уравнения прямой, записанное в такой форме, называется также каноническим. Вектор а{l,m,n} называют направляющим вектором.
3. Уравнение прямой, проходящей через две точки М1(х1,y1,z1) и М2(х2,y2,z2)
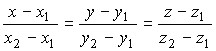
Уравнение получено из условия параллельности двух векторов:
![]()
![]()
Рекомендация. Изучить самостоятельно разделы «Уравнение прямой в проекциях», «Параметрические уравнения прямой».
Пример
Дано уравнение прямой 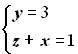
Найти направляющий вектор.
Решение:
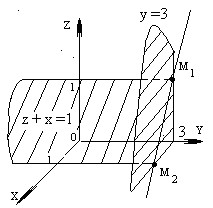
Построим плоскости. Пусть точки M1(x1, y1, z1) и М2(x2, y2, z2) принадлежат обеим плоскостям, M1M2 — отрезок искомой прямой. Найдем координаты M1 и М2. Пусть М1 — точка пересечения искомой прямой с плоскостью ZOY, тогда x1 = 0. Согласно данному уравнению прямой y = 3; z = 1, следовательно, М1 (0; 3; 1). Пусть М2 — точка пересечения искомой прямой с плоскостью XOY, следовательно, z = 0, тогда х = 1, у = 3, при этом М2 (1;3;0).
Уравнение прямой, проходящей через две точки, имеет вид
![]()
Представим данное уравнение в канонической форме
![]()
Из полученного уравнения определяется направляющий вектор
![]()
Спонсор статьи — Ing-Grafika — ваш лучший помощник в начертательной геометрии и инженерной графике. Здесь вы можете заказать чертежи любого формата по доступным ценам. Кроме того, на сайте Ing-Grafika вы найдете тематические учебники, самоучители, ГОСТы, видеоуроки и многое другое. С нами в вашей зачетке напротив графы «Начертательная геометрия 1 курс» просто не может стоять ничего, кроме твердого «отлично».