В мире математики существует множество интересных и удивительных концепций. Одним из математических феноменов стали числа Фибоначчи. Эта математическая последовательность имеет множество применений и связей с различными областями науки, искусства и природы.
Кто такой Фибоначчи

Леонардо Пизанский, более известный как Фибоначчи, был итальянским математиком XIII века. Он считается одним из самых выдающихся математиков средневековой Европы и внес значительный вклад в развитие математической науки, в том числе введение арабских чисел в европейскую математику.
Важный факт: математик стал известен благодаря своей книге «Liber Abaci» (1202 г.), которая была посвящена арифметике и включала описание последовательности чисел, позже названных в его честь.
Последовательность Фибоначчи
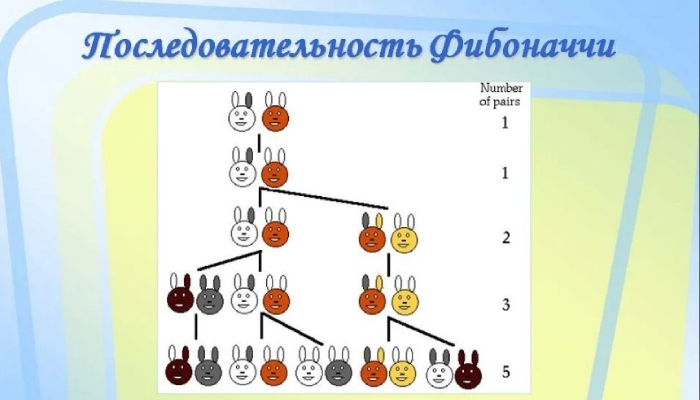
Имеется в виду числовой ряд, где каждое значение является суммой двух предыдущих чисел, начиная с 0 и 1. Таким образом, последовательность выглядит следующим образом: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее.
Интересный факт: задача про кроликов — это классическая задача, в которой феноменальный математический ряд был впервые использован для описания роста популяции кроликов. Это одно из самых известных применений последовательности знаменитого математика.
Где используются числа Фибоначчи

Они нашли широкое применение в различных областях:
- Математика: последовательность служит основой для многих математических задач и теорем.
- Компьютерная наука: они используются в алгоритмах, связанных с оптимизацией и обработкой данных.
- Финансы: применяется в техническом анализе для предсказания поведения рынка и определения уровней поддержки и сопротивления.
- Биология: последовательность Фибоначчи наблюдается в росте и размножении некоторых живых организмов.
Применение этой закономерности в архитектуре является еще одним интересным аспектом этого математического открытия. Здания, созданные на их основе, обладают особым эстетическим очарованием и гармонией. Например, пирамиды Гизы и Парфенон в Афинах были спроектированы с использованием этих пропорций.
В природе этот математический феномен также встречаются повсюду. Расположение ветвей деревьев, структура кристаллов и снежинок, устройство молекул ДНК – все это лишь некоторые из многочисленных примеров присутствия этой последовательности в окружающем мире. Такая универсальность чисел Фибоначчи свидетельствует о глубоких закономерностях, лежащих в основе природы и математики.
Современные исследования продолжают раскрывать новые области их применения. Например, в области компьютерного моделирования и графики эта феноменальная закономерность используются для создания реалистичных изображений и анимации, которые эффективно имитируют реальные сцены и объекты.
В криптографии эта математическая последовательность чисел Фибоначчи также играет важную роль. Она используются в различных алгоритмах шифрования и генерации случайных значений, что обеспечивает повышенную степень защиты данных и информации. Это свидетельствует о том, что числа Фибоначчи остаются актуальными и важными в наше время, также как, например, в русском языке разряды местоимений.
В области физики феномен применяется для изучения квантовых явлений, таких как переплетение и декогеренция. Эти числа также обнаружены в нанотехнологиях, где они определяют определенные характеристики кристаллических структур и молекулярных связей.
В области экономики последовательность также оказывает влияние на фундаментальные принципы и стратегии управления финансовыми ресурсами. В экономической теории и моделировании эти числа используются для анализа финансовых рынков и прогнозирования экономических циклов, что способствует более эффективному и точному управлению рисками и инвестициями.
В биологии это математическое явление имеет существенное значение, особенно в изучении генетики и морфологии различных организмов. Распределение чисел Фибоначчи в структуре хромосом и молекул ДНК указывает на определенные закономерности наследственности и эволюции, что помогает ученым лучше понять процессы развития и адаптации живых систем.
Интересный факт: в музыке числа Фибоначчи и золотое сечение используются для создания гармоничных и пропорциональных музыкальных структур, таких как аккорды, ритмы и мелодии.
Что такое золотое сечение
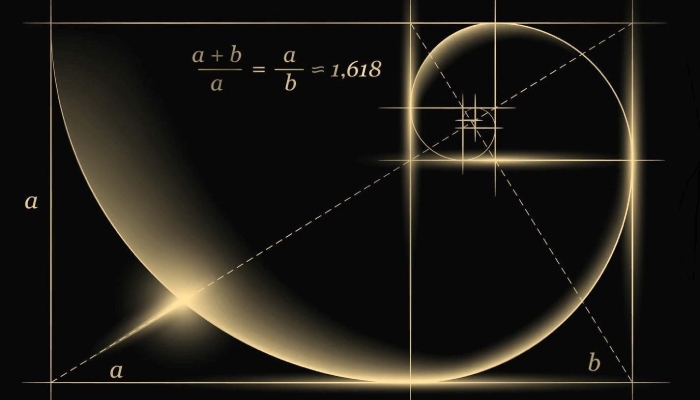
Золотое сечение является математическим принципом, который обозначает пропорцию, в которой сумма двух величин равна отношению большей величины к меньшей. Это отношение (примерно 1,618) известно как «золотое число» или φ (греческая буква «фи»). Оно связано с рядом Фибоначчи, так как отношение двух последовательных чисел стремится к золотому сечению с увеличением чисел последовательности. Золотое сечение имеет множество применений в архитектуре, искусстве, дизайне и природе, где оно часто ассоциируется с гармонией и эстетической привлекательностью.
Интересный факт: Золотое сечение часто использовалось выдающимися художниками, такими как Леонардо да Винчи и Сальвадор Дали, для достижения эстетической гармонии и пропорций в своих произведениях.
Что такое спираль Фибоначчи
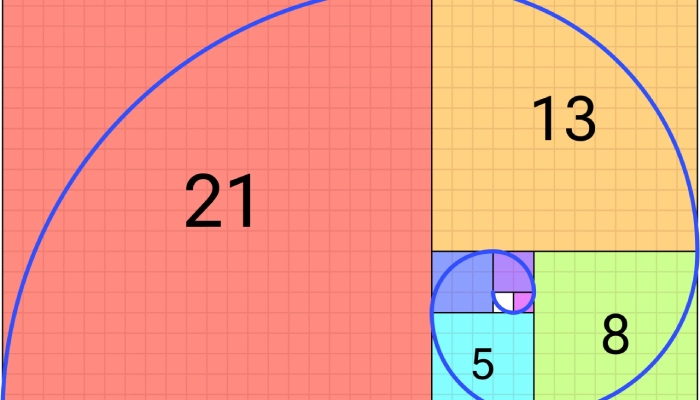
Визуальное представление феноменального ряда чисел Фибоначчи — это геометрическая форма, основанная на числах Фибоначчи и золотом сечении. Она представляет собой набор четырехугольников, у которых стороны равны числам Фибоначчи, и которые соединяются таким образом, что образуют спираль. Спираль также назвали в честь средневекового математика. Ее можно наблюдать в природе, например, в расположении листьев на стебле, семенах подсолнечника или раковинах моллюсков.
Важный факт: Спираль Фибоначчи обнаружена даже в галактиках, где она прослеживается в структуре вращающихся спиральных галактик, что указывает на глубокую связь между математическими принципами и космическими явлениями.
Ряд Фибоначчи является уникальным и удивительным явлением в математике, которое имеет множество применений и связей с другими областями науки, искусства и природы. От золотого сечения до спирали Фибоначчи, эти числа продолжают вдохновлять ученых, инженеров и художников на создание новых идей и открытий, подтверждая гармоничное взаимодействие математики и окружающего мира.