Теорема Менелая — это одна из основных теорем в геометрии, которая связывает отношения длин отрезков на сторонах треугольника. Названа в честь французского математика Герарда Менелая.
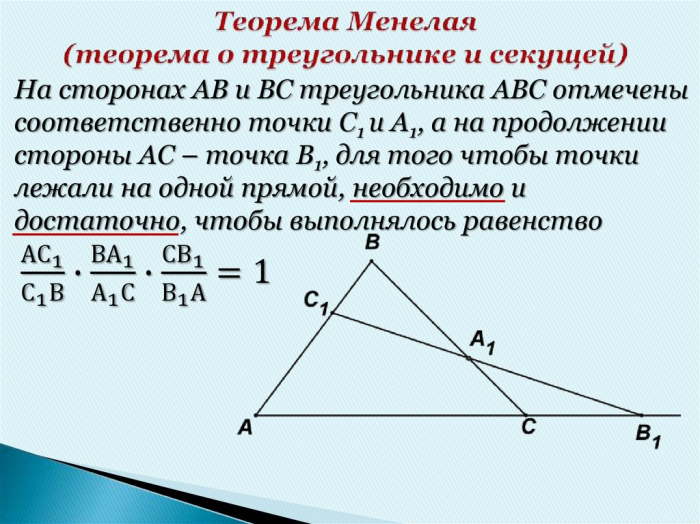
Теорема утверждает, что если точки A, B и C лежат на одной прямой и D, E и F являются произвольными точками на сторонах AB, BC и CA соответственно, то выполняется следующее условие:
AD/DB × BE/EC × CF/FA = 1
Это равенство позволяет нам выражать отношения длин сегментов в треугольнике через другие известные длины. Также теорема Менелая может быть использована для вывода других геометрических результатов.
Рассмотрим пример применения теоремы Менелая:
Задача:
«В трех заданных точках A, B и C проведены произвольные отрезки AD, BE и CF такие,
что они пересекаются в одной точке G. Докажите, что отрезки AG/GB, BG/GC и CG/GA
удовлетворяют условию теоремы Менелая.»
Доказательство данной задачи можно провести с использованием теоремы Менелая и доказать равенство отношений длин указанных сегментов.
Знакомство с теоремой Менелая
Теорема Менелая – это одна из фундаментальных теорем в геометрии, которая описывает отношения длин отрезков на сторонах треугольника. Теорема названа в честь Герарда Менелая, французского математика XVII века.
Суть теоремы заключается в следующем:
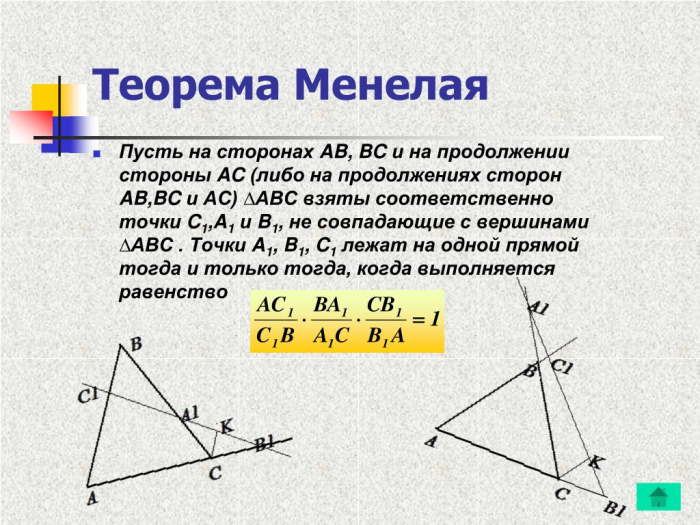
Если точки A, B и C лежат на одной прямой и D, E и F являются произвольными точками на сторонах AB, BC и CA соответственно, то выполняется следующее условие:
AD/DB × BE/EC × CF/FA = 1
Такое равенство позволяет выражать отношения длин сегментов через другие известные длины. Также теорему Менелая можно использовать для вывода других геометрических результатов.
Для более полного понимания работоспособности данной теоремы рассмотрим пример её применения:
Задача:
«В треугольнике ABC проведены медианы AD, BE и CF. Докажите, что они пересекаются в одной точке.»
Решение данной задачи основывается на применении теоремы Менелая для отношений длин сегментов медиан.
Таким образом, теорема Менелая является мощным инструментом в геометрии и позволяет решать различные задачи, связанные с треугольниками и отношениями длин его сторон.
Основные понятия
Для полного понимания теоремы Менелая важно ознакомиться с некоторыми основными понятиями:
Треугольник – это геометрическая фигура, состоящая из трех отрезков, называемых сторонами, и трех вершин.
Отношение длин двух отрезков можно выразить как частное их длин. Например, если отрезок AB имеет длину 3 единицы, а отрезок CD – 2 единицы, то отношение длин будет равно 3/2 или 1.5.
Пропорциональность. Говорят, что четыре числа a, b, c и d пропорциональны (обозначается a:b = c:d), если и только если их отношения равны: a/b = c/d. Пропорциональные числа обладают одинаковым соотношением между собой.
Mенелаевское соотношение – это равенство, которое выражает отношения длин сегментов на сторонах треугольника через произведение этих отношений. Основная формула Менелая имеет вид: AD/DB × BE/EC × CF/FA = 1.
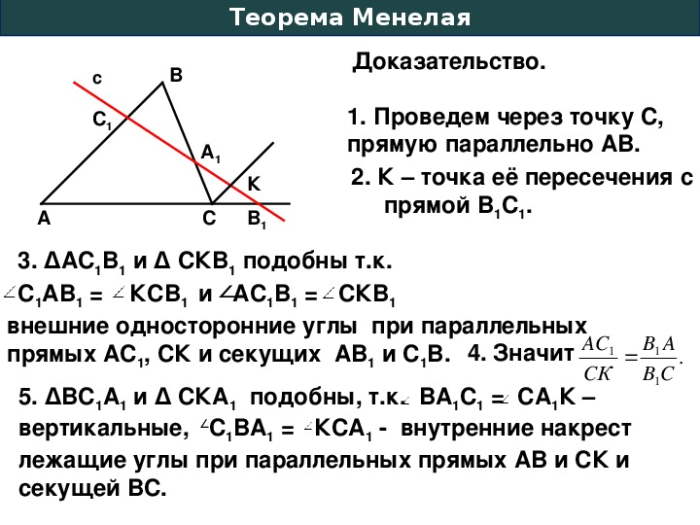
Доказательство. В математике доказательство – это логическая последовательность утверждений, позволяющих убедиться в истинности какого-либо утверждения или теоремы. Для доказательства теоремы Менелая используются геометрические рассуждения и свойства треугольников.
Изучив эти основные понятия, вы будете готовы к более глубокому изучению теоремы Менелая и применению её в задачах по геометрии.
Что такое треугольник и какие величины в нем играют роль
Треугольник – это геометрическая фигура, состоящая из трех отрезков, называемых сторонами, и трех вершин. Он является одной из основных форм в плоской геометрии.
В треугольнике существуют различные величины, которые играют ключевую роль при применении теоремы Менелая:
Стороны треугольника обозначаются буквами a, b и c. Они являются отрезками между вершинами и определяют его форму и размеры.
Углы треугольника обозначаются заглавными буквами A, B и C. Они находятся между сторонами треугольника и определяют его форму.
Медианы – это отрезки, соединяющие каждую вершину треугольника с серединой противоположной стороны. Обозначаются буквами AD, BE и CF.
Периметр треугольника – это сумма длин его сторон. Обозначается буквой P.
Площадь треугольника – это мера его поверхности. Вычисляется по формуле: S = 1/2 × основание × высота или используя формулу Герона для треугольников со всеми сторонами известными.
Изучение этих величин поможет вам лучше понять свойства и способы решения задач, связанных с теоремой Менелая и геометрией в целом.
Примеры применения теоремы Менелая
Теорема Менелая является мощным инструментом в геометрии и может быть использована для решения различных задач. Рассмотрим некоторые примеры её применения:
Задача 1:
«В треугольнике ABC проведены медианы AD, BE и CF. Докажите, что они пересекаются в одной точке.»
Решение данной задачи основывается на применении теоремы Менелая для отношений длин сегментов медиан: AD/DB × BE/EC × CF/FA = Подставив известные значения отношений длин (которые равны 2:1), можно утверждать, что эти отрезки пересекаются в одной точке.
Задача 2:
«В треугольнике ABC проведены высоты AD, BE и CF. Докажите, что они также пересекаются в одной точке.»
Аналогично предыдущей задаче, для решения данного случая можно использовать ту же формулу Менелая. Но в данном случае отношения длин будут зависеть от высот треугольника.
Также теорема Менелая может быть применена для решения задач, связанных с расположением точек на сторонах треугольника или поиску соотношений между длинами сегментов.
Приведенные примеры лишь небольшая часть возможных задач и приложений теоремы Менелая. Она играет важную роль в геометрии и помогает понять свойства треугольников и отношения между их сторонами.