Площадь параллелограмма — одна из основных характеристик этой геометрической фигуры. Нахождение площади параллелограмма является важной задачей, которая требует применения определенных формул и понимания основных принципов. В данном тексте рассмотрим методику расчета площади параллелограмма и приведем примеры для более наглядного представления.
Формулы для расчета площади параллелограмма
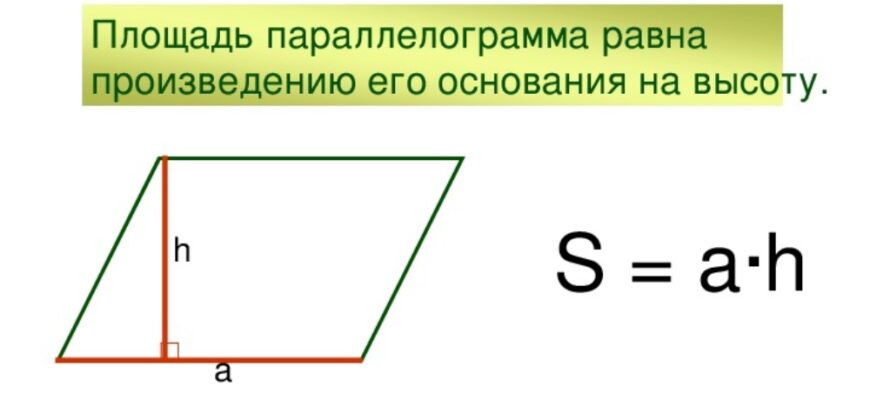
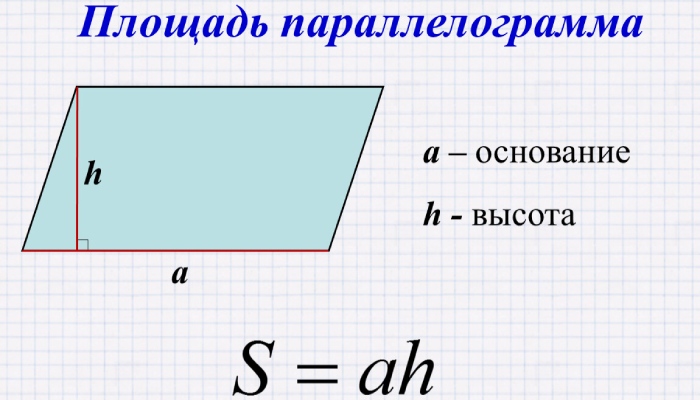
Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны и равны в длину. Площадь параллелограмма можно найти по формуле:
S a * h
где S — площадь параллелограмма, a — длина одной из сторон, h — высота (перпендикулярная проведенная к этой стороне).
Также, можно использовать формулу:
S b * c * sin(α),
где b и c — две соседние стороны параллелограмма, α — угол между этими сторонами.
Бывают случаи, когда значения не даны явно, а заданы координатами вершин A(x1,y1), B(x2,y2), C(x3,y3) и D(x4,y4), то можно воспользоваться следующей формулой:
S |(x2-x1)*(y3-y1)-(x3-x1)*(y2-y1)|
Примеры решения задач
Пример 1
Найдем площадь параллелограмма со сторонами 5 и 8 см и высотой 4 см.
- Решение:
- a 5
- h 4
- S a * h 5 * 4 20 см²
Пример 2
Найдем площадь параллелограмма со сторонами 6 и 9 см и углом между ними 60 градусов.
- Решение:
- b 6
- c 9
- α 60° (угол между сторонами b и c)
- S b * c * sin(α) 6 * 9 * sin(60°) ≈ 23.38 см²
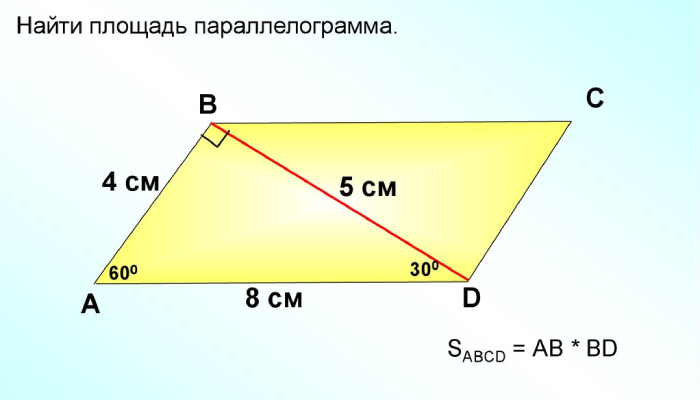
Пример 3
Параллелограмм ABCD имеет координаты вершин A(-5,-3), B(-2,-5), C(7,-7) и D(10,-5). Найдем его площадь.
Сначала найдем коэффициенты наклона AB и CD:
kAB (-5 2)/(-3 5) -0.33
kCD (10-7)/(-5 7) 0.33
Затем рассчитаем уравнения прямых AB и CD:
y -0.33x — 0.67
y 0.33x — 4.67
Найдем точку пересечения этих прямых, она будет являться вершиной параллелограмма:
-0.33x — 0.67 0.33x — 4.67
x (4-(-7))/(0,33 (-0,33)) ≈ 3
y -0,33*3-6/3-2
Таким образом, вершина BCD находится в точке (3,-2). Аналогичным образом находим координаты вершины A.
kAD(-5-10)/(-3 5)-7/2;
kBC(-2 7)/(-5 7)1;
Значит уравнения прямых AD и BC имеют вид:
y-7/2*x-b1
y1*x b2,
где b1,b2 — свободный член.
Из системы двух линейных уравнений можно найти координаты пересечения прямых:
b1y-a*x,
b2y c*x.
Решив эту систему методом подстановок или методом Крамера получаем значения x28/15; y49/15.
После этого можно вычислить длину одной из сторон (например, AB) как расстояние между точками A и B:
ABsqrt((-5—2)^2 (-3—5)^2)sqrt(34)
Высота h, проведенная к стороне AB, равна расстоянию от точки C до прямой AB. Для этого найдем уравнение прямой, проходящей через A и B:
y (-5 3)/( — 2 5)x — 3
y -0.67x — 1.99
Теперь найдем координаты пересечения этой прямой с CD:
-0.67x — 1.99 0.33x — 4.67
x ≈ 7
y ≈ -6
Таким образом, высота h равна расстоянию между точками C и (7,-6):
hsqrt((7-(-5))^2 (-7-(-6))^2)≈13.
И наконец можно рассчитать площадь параллелограмма по формуле SAB*h:
S ≈ sqrt(34)*13 ≈44 (квадратных единицы).