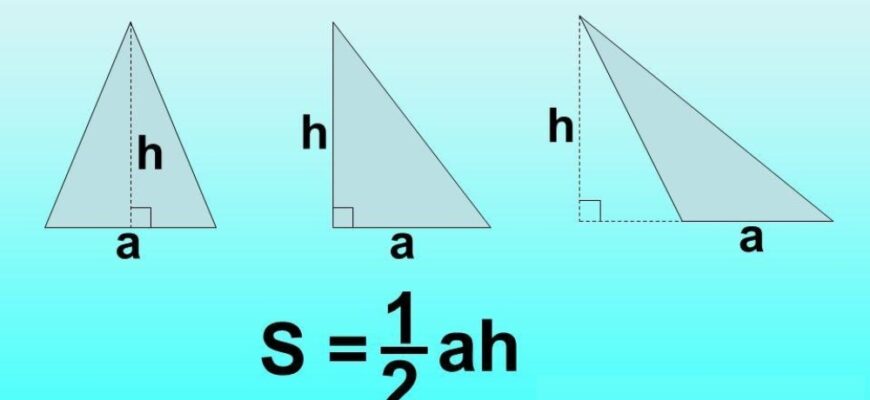
Треугольник — это геометрическая фигура, которая имеет три стороны и три угла. Свойства треугольника изучаются в школе на уроках геометрии.
Существует несколько видов треугольников:
- Равносторонний, у которого все стороны равны;
- Равнобедренный, который имеет две равные стороны;
- Прямоугольный, у которого один из углов прямой (равен 90 градусам);
- Остроугольный, все его углы острые;
- Тупоугольный, один из его углов тупой (более 90 градусов).
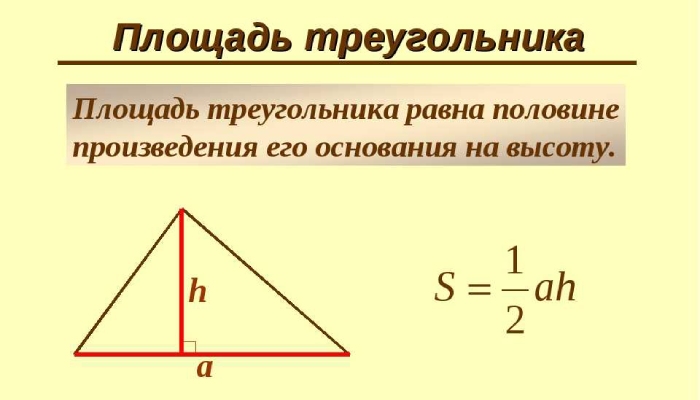
Площадь треугольника может быть вычислена по формуле:
S = 0.5 * a * h
- a — длина основания треугольника;
- h — высота, опущенная на основание.
Примеры на нахождение площади треугольника
Пример 1:
Дан треугольник со сторонами:
- a — 4 см;
- h — 6 см.
Найдем площадь данного треугольника:
S = 0.5 * 4 * 6
S = 12 см².
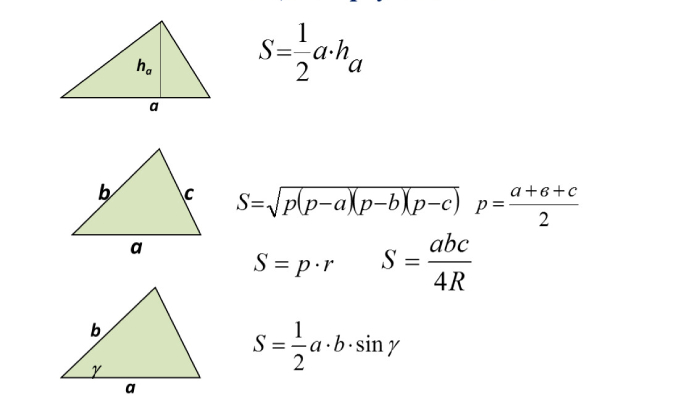
Пример 2:![]()
Треугольник ABC со сторонами a, b и c. Найти площадь треугольника abc.
- a — 10 см;
- b — 8 см;
- c — 6 см;
Мы можем найти высоту треугольника, по формуле Герона:
p =(a b c) / 2 (10 8 6) / 2
S = √( p * (p-a) * (p-b) *(p-c))
S = √(12*(12-10)*(12-8)*(12-6))
S ≈ 23.76 см².
Вывод
Площадь треугольника — это основная характеристика данной геометрической фигуры. Она может быть найдена по формуле, которая зависит от длины сторон и высоты, опущенной на основание. Знание этой формулы является важным элементом в математике и физике.