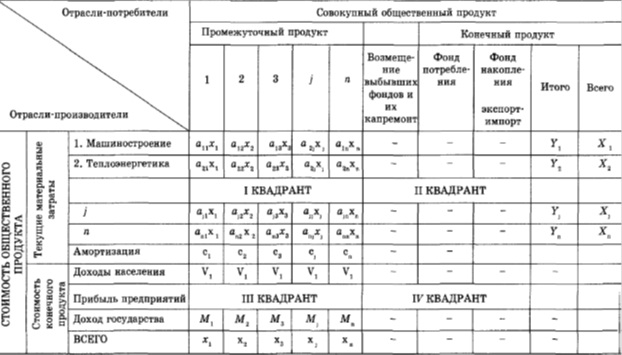
Таблица МОБ (межотраслевого баланса) позволяет изучать структуру потоков ресурсов. Однако для понимания функционирования экономики, в частности, эффекта распространения (мультипликации), необходимо сделать еше один шаг, заключающийся в построении коэффициентов прямых затрат и коэффициентов полных затрат, Будем, следуя автору модели, американскому ученому русского происхождения В.Леонтьеву, считать, что объемы промежуточного производственного потребления прямо пропорциональны объемам производства продукции потребляющих отраслей:
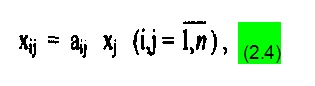
где коэффициентами пропорциональности aij являются коэффициенты прямых материальных затрат, определяемые из соотношений:
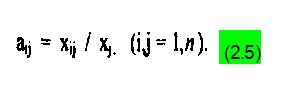
Из (2.4) следует и смысл этих коэффициентов; они показывают объем материальных ресурсов i-го вида, необходимый для производства единицы валового продукта j -го вида. После подстановки (2.4) в (2.1) получаем
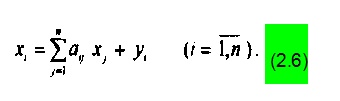
Это и есть система уравнений модели В.Леонтьева «затраты — выпуск», называемая статической моделью МОБ. Статической она является потому, что отражает производство и основные потоки продукции между отраслями за фиксированный промежуток времени (обычно за год), в течение которого все параметры модели остаются постоянными.
Получив систему уравнений (2.6), мы вплотную подошли к центральному вопросу межотраслевого анализа; как изменится объем валового выпуска i-й отрасли (Xi), если при фиксированных коэффициентах прямых затрат аij значение уi изменится на величину дельта уi.
Отметим, что соотношение (2.5) предполагает существование производственной функции с неизменным эффектом масштаба (затраты прямо пропорциональны выпуску) и с отсутствием взаимозаменяемости ресурсов соотношение затрат ресурсов фиксировано и не зависит от уровня выпуска). Кроме того, здесь учитываются только затраты промежуточных продуктов, затраты факторов производства опущены. Для ответа на поставленный вопрос необходимо найти решение Xi (i = 1,n) системы линейных уравнений (2.6) при фиксированных значениях спроса на конечную продукцию уi (i = 1,n).
Запишем систему уравнений (2.6) в матричной форме: