Метод анализа иерархий. Дополнительные приложения МАИ

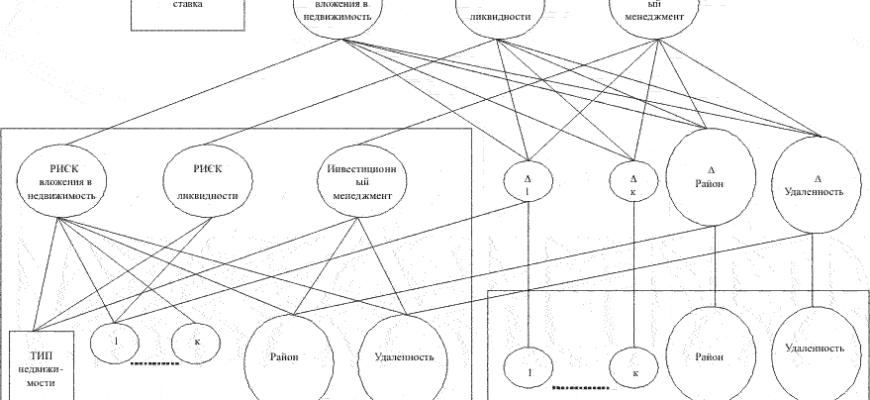
А. ВЫБОР РАБОТЫ

Со студентом, только что получившим диплом, беседовали о трех возможных местах работы (А, Б и В). Он решил использовать МАИ для осуществления выбора. Иерархия этого примера — полная.

Критерии студента для выбора работы и соответствующая матрица парных сравнений представлены в табл.3.9 вместе с собственным вектором (нормализованным), связанным с максимальным собственным значением. В этой матрице пары критериев сравниваются с точки зрения их относительного вклада в общее понятие «удовлетворение работой». Задавался вопрос: который из заданной пары критериев представляется вносящим большой вклад в понятие «удовлетворение работой» и насколько? Например, число 5 в третьей строке и четвертом столбце показывает, что «доходы» намного важнее, чем «общество коллег».

Таблица 3.9. Матрицы попарных сравнений для выбора работы

Индекс согласованности равен 0,07

Полученные собственные векторы (один из каждого критерия) взвешиваются с помощью соответствующей компоненты собственного вектора объединенного критерия, и результаты суммируются и нормализуются. 

Краткое изложение этапов МАИ

Будет полезным еще раз повторить этапы МАИ. Отдельным этапам можно уделять больше внимания в одних ситуациях, чем в других.

1. Очертите проблему и определите, что вы хотите узнать.
2. Постройте иерархию, начиная с вершины (цели — с точки зрения управления), через промежуточные уровни (критерии, по которым зависят последующие уровни) к самому нижнему уровню (который обычно является перечнем альтернатив).
3. Постройте множество матриц парных сравнений для каждого из нижних уровней — по одной матрице для каждого элемента примыкающего сверху уровня. Этот элемент называют направляемым по отношению к элементу, находящемуся на нижнем уровне, так как элемент нижнего уровня влияет на расположенный выше элемент. В полной простой иерархии любой элемент воздействует на каждый элемент примыкающего сверху уровня. Элементы любого уровня сравниваются друг с другом относительно их воздействия на направляемый элемент. Таким образом, получаем квадратную матрицу суждений. Попарные сравнения проводятся в терминах доминирования одного из элементов над другим. Эти суждения затем выражаются в целых числах (см. табл. 3 для величин суждений). Если элемент А доминирует над элементом Б, то клетка, соответствующая строке А и столбцу Б, заполняется целым числом, а клетка, соответствующая строке Б и столбцу А, заполняется обратным к нему числом (дробью). Если элемент Б доминирует над элементом А, то происходит обратное: целое число ставится в позицию Б, А, а обратная величина автоматически в позицию А, Б. Если считается, что А и Б одинаковы, в обе позиции ставится единица.
4. На этапе 3 для получения каждой матрицы требуется n(n-1)/2 суждений (напомним, что при каждом парном сравнении автоматически приписываются обратные величины).
5. После проведения всех парных сравнений и ввода данных по собственному значению можно определить согласованность. Затем, используя отклонение λ_max от п, проверяем индекс согласованности, далее, сравнивая с соответствующими средними значениями для случайных элементов, получаем отношение согласованности.
6. Этапы 3, 4 и 5 проводятся для всех уровней и групп в иерархии.

1      Теперь используется иерархический синтез для взвешивания собственных векторов весами критериев и вычисляется сумма по всем соответствующим взвешенным компонентам собственных век торов уровня иерархии, лежащего ниже.

2      Согласованность всей иерархии можно найти, перемножая каждый индекс согласованности на приоритет соответствующего критерия и суммируя полученные числа. Результат затем делится на выражение такого же типа, но со случайным индексом согласованности, соответствующим размерам каждой взвешенной приоритетами матрицы. Отметим, во-первых, что приемлемым является ОС около 10% или менее. В противном случае качество суждений следует улучшить, возможно пересмотрев способ, следуя которому задаются вопросы при проведении парных сравнений. Если это не поможет улучшить согласованность, то, вероятно, задачу следует более точно структурировать, т.е. сгруппировать аналогичные элементы под более значащими критериями. Потребуется возврат к этапу 2, хотя пересмотра могут потребовать только сомнительные части иерархии. (Читатель может вычислить согласованность иерархии в примере покупки дома и получить величину 0,081, что приемлемо.)

При проведении оценок следует иметь в виду все сравниваемые элементы, чтобы сравнения были релевантными. Нетрудно убедиться в том, что для проведения обоснованных численных сравнений не следует сравнивать более чем 7±2 элементов. В таком случае маленькая погрешность в каждой относительной величине меняет ее не очень значительно. В случае более широкого класса объектов применяется иерархическая декомпозиция. Элементы группируются (в качестве первой оценки) в сравниваемые классы приблизительно из семи элементов в каждом. Элемент с наивысшим весом в классе также включается в следующий класс элементов с большими весами и как своеобразный стержень между двумя классами придает однородность шкале. Процедура повторяется от одного класса к смежному классу, пока все элементы не будут взвешены соответствующим образом.

В некоторых задачах с большим числом альтернатив нам не всегда нужно проводить парные сравнения между ними. Вместо этого вводим субкритерии (например, высокий, средний, низкий) и устанавливаем важность этих субкритериев по отношению к критериям. Затем берем каждую альтернативу, проверяем, который из субкритериев описывает ее наилучшим образом, и принимаем приоритет этого субкритерия. Далее складываем все приоритеты для этой альтернативы, и, наконец, нормализуем величины альтернатив, чтобы получить их общий приоритет.