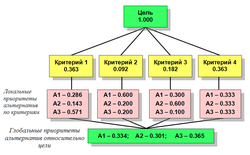
На этом этапе в нашем примере семья построила иерархию, составила матрицы и выразила субъективные парные суждения. Как они помогут определить тот дом, который следует купить? В этом разделе описывается, каким образом сочетаются иерархическая декомпозиция и шкала относительной важности для получения осмысленных подходов к многокритериальным проблемам планирования.
А. СИНТЕЗ: ЛОКАЛЬНЫЕ ПРИОРИТЕТЫ
Из группы матриц парных сравнений мы формируем набор локальных приоритетов, которые выражают относительное влияние множества элементов на элемент примыкающего сверху уровня. Находим относительную силу, величину, ценность, желательность или вероятность каждого отдельного объекта через «решение» матриц, каждая из которых обладает обратносимметричными свойствами. Для этого нужно вычислить множество собственных векторов для каждой матрицы, а затем нормализовать результат к единице, получая тем самым вектор приоритетов.
Вычисление собственных векторов — не очень сложная задача, однако может потребовать довольно много времени. К счастью, имеются несложные пути получения хорошего приближения к приоритетам. Одним из наилучших путей является геометрическое среднее. Это можно сделать, перемножая элементы в каждой строке и извлекая корни п -й степени, где п — число элементов. Полученный таким образом столбец чисел нормализуется делением каждого числа на сумму всех чисел. Иной способ заключается в нормализации элементов каждого столбца матрицы и затем в усреднении каждой строки. Таким образом, мы можем определить не только порядок приоритетов каждого отдельного элемента, но и величину его приоритета.
При использовании любого метода аппроксимации существует опасность изменения порядка ранжирования и поэтому получения нежелательных результатов. Подход, основанный на собственном векторе, использует информацию, которая содержится в любой, даже несогласованной матрице, и позволяет получать приоритеты, основанные на имеющейся информации, не производя арифметических преобразований данных. Для индивидуума или группы лиц идея заключается в том, чтобы решить, хотят они или нет изменить суждения.
Далее выполняется умножение матрицы суждений на вектор приоритетов:
Когда матрица имеет такой вид, получается, что в действительности х1, х2, х3 и х4 есть не что иное, как w1, w2, w3 и w4 соответственно. Из отношений wi/wj можно определить каждую компоненту w. Важно отметить, что в матрице суждений нет отношения в виде wi/wj, а имеются только целые числа или их обратные величины из шкалы. Эта матрица в общем случае несогласованна.
Алгебраически задача в случае согласованности заключается в решении уравнения Aw = nw, А = (wi/wj), а общая задача с обратносимметричными суждениями заключается в решении уравнения А‘ w‘ = λmaxw‘, А‘ = (аij), где λmax — наибольшее собственное значение матрицы суждений А.
Б. СОГЛАСОВАННОСТЬ ЛОКАЛЬНЫХ ПРИОРИТЕТОВ ‘
Весьма полезным побочным продуктом теории является так называемый индекс согласованности (ИС), который дает информацию о степени нарушения численной (кардинальной, аijаjk = аik) и транзитивной (порядковой) согласованности. Для улучшения согласованности можно рекомендовать поиск дополнительной информации и пересмотр данных, использованных при построении шкалы. В других процедурах построения шкал отношения нет структурно порожденного индекса.
Все измерения, включая те, в которых используются приборы, подвержены погрешностям измерений, а также погрешностям из-за неточностей в самом измерительном приборе. Эти погрешности могут привести к несогласованным выводам. Например, при взвешивании предметов измерения могут показать, что А тяжелее, чем Б, Б тяжелее, чем В, однако В тяжелее, чем А. В частности, это может случиться, когда веса предметов А, Б и В близки, а прибор недостаточно точен, чтобы их различить. Отсутствие согласованности может быть серьезным ограничивающим фактором для исследования некоторых проблем, но не быть таковым для других. Например, если объекты — два химиката, которые должны быть смешаны в точных пропорциях при изготовлении лекарства, то несогласованность может означать, что в пропорции применяется один химикат в большем, чем необходимо, количестве, что, возможно, приведет к вредным последствиям при употреблении лекарства.
Однако совершенной согласованности при измерениях даже с наиболее точными инструментами трудно достичь на практике. Нужен способ оценки степени согласованности при решении конкретной задачи.
Вместе с матрицей парных сравнений мы имеем меру оценки степени отклонения от согласованности. Когда такие отклонения превышают установленные пределы, тому, кто проводит суждения, следует перепроверить их в матрице.
Индекс согласованности в каждой матрице и для всей иерархии может быть приближенно получен вычислениями вручную. Сначала суммируется каждый столбец суждений, затем сумма первого столбца умножается на величину первой компоненты нормализованного вектора приоритетов, сумма второго столбца — на вторую компоненту и т. д. Затем полученные числа суммируются. Таким образом можно получить величину, обозначаемую λmax . Для индекса согласованности имеем ИС = (λmax — n) / (n-1), где n — число сравниваемых элементов. Для обратносимметричной матрицы всегда λmax ≥ n