Особенностью развития современного российского общества является сложный характер рыночной экономики,
характеризуемый изменением и быстрой сменяемостью условий экономической деятельности, предъявлением высоких требований к методам планирования и хозяйственной деятельности. Математическое моделирование экономических ситуаций позволяет определить мероприятия, обеспечивающие необходимую эффективность производства или предпринимательства, и на основе этих данных принять решение о выборе оптимальной стратегии по управлению бизнесом.
В повседневной жизни мы часто сталкиваемся с необходимостью решать оптимизационные задачи. Например, заходя в магазин, мы стоим перед дилеммой максимального удовлетворения своих потребностей, соизмеряя их с возможностями нашего кошелька. Любой менеджер постоянно решает разнообразные проблемы, начиная с планирования штата сотрудников, фонда зарплаты и заканчивая составлением оптимального плана производства, планированием рекламной кампании по продвижению продукции и оптимизацией капиталовложений. При военных действиях командиры решают задачи оптимального указания целей и наведения оружия на эти цели в расчете на максимальное поражение противника. Менеджер по транспортным перевозкам решает задачу минимизации транспортных издержек в условиях наиболее полного удовлетворения интересов производителей и потребителей.
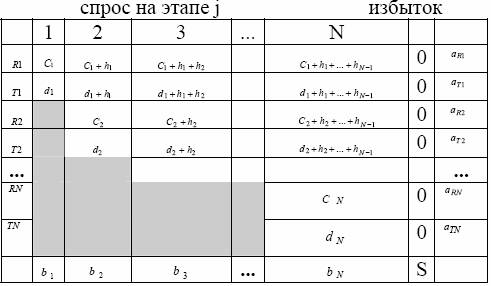
Настоящая работа посвящена знакомству с одной из самых популярных и востребованных экономико-математических моделей — транспортной задаче. Транспортная задача представляет собой задачу линейного программирования, однако ее специфическая структура позволяет так модифицировать симплекс-метод, что вычислительные процедуры становятся более эффективными.
В классической транспортной задаче рассматриваются перевозки (прямые или с промежуточными пунктами) одного или нескольких видов продукции из исходных пунктов в пункты назначения. Эту задачу можно видоизменить, включив в нее ограничения сверху ни пропускные способности транспортных коммуникаций. Но так же как задачу транспортного типа можно рассматривать задачу о назначениях и задачу управления запасами.
